1. À l'ère du numérique
Réflexions
Un mystère à éclaircir
Comment, un appareil photo numérique, une calculette, un ordinateur, un téléphone portable… peuvent-ils traiter de l'information, c'est-à-dire la capturer, la transformer et la diffuser, par le simple fait qu'un courant électrique se propage dans certains circuits et pas dans d'autres?
Tous ces appareils possèdent une mémoire et celle-ci est composée de millions, voire de milliards de circuits électroniques interconnectés par des commutateurs (des interrupteurs, si vous préférez).
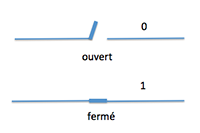
Ces commutateurs ont deux états possibles : ouvert ou fermé ou encore : 0 ou 1. En position 0, le courant ne circule pas; en position 1, il circule.

En faisant un petit effort d'imagination, on peut donc considérer que cette mémoire est assimilable à un vaste ensemble de 0 et de 1.
Cela signifie que la seule information qui puisse être traitée par ces appareils doit pouvoir s'exprimer comme une suite de 0 et de 1. Voilà pourquoi on dit que toute l'information qui est traitée par ces appareils est numérique. Seules sont traitables, les informations qui peuvent être assimilées à des 0 et des 1 et rien d'autre !
Mais un texte, une image, un air de musique, cela ne ressemble pas du tout à des 0 et des 1. Alors, posons-nous la question de savoir comment ils peuvent le devenir. Cela nous aidera à comprendre quelles sont les limites du traitement de l'information numérique.
Commençons par quelque chose de simple.
Transformer un nombre entier en 0 et en 1
Pouvez-vous proposer une manière de faire ? Que deviendrait le chiffre 4 ou le nombre 13 si on cherchait à les transformer en suites de 0 et de 1 ?
Le truc est fastoche ! Comptons comme nous en avons l'habitude, dans notre système décimal, avec nos dix chiffres. Puis, parallèlement, comptons comme si nous ne disposions que de 0 et de 1, dans un système binaire car il ne comprend que deux chiffres.

À chaque fois que nous avons épuisé toutes les possibilités pour un chiffre à une des positions, nous le ramenons à zéro et augmentons le chiffre de la position à sa gauche (après 1, 10; après 11, 100; après 101, 110; après 111, 1000 et ainsi de suite). Il vous suffit d'imaginer un compteur kilométrique de voiture qui n'utiliserait que deux chiffres.
On voit que le nombre 4 (en décimal) s'écrit 100 (en binaire), le nombre 11 devient 1011. Le nombre 13 deviendra 1101. On dira que ce nombre 1101 est composé de quatre chiffres binaires (en anglais, binary digit ou bits). C'est un nombre de quatre bits.
Dans le système binaire, chaque chiffre d'un nombre binaire est appelé bit. C'est la contraction de l'expression anglaise « binary digit » qui signifie littéralement « chiffre binaire ».
Avant de vous lancer dans les activités, voici deux questions pour vous permettre de vérifier si vous avez compris.
Quel est le nombre binaire qui succédera à 100111001 ? Et quel est celui qui succédera à 10101111 ?
100111010
10110000
Terminons par une conclusion importante :
Nous avions déjà compris qu'une information est traitable par un ordinateur si on peut la transformer en une suite 0 et1.
Désormais, comme il y a une correspondance entre le système binaire et notre système décimal, nous pouvons affirmer :
une information est traitable par un ordinateur, si on peut la transformer en une suite de nombres entiers.
Dans les activités qui suivent, vous allez essayer d'inventer des façons de numériser des nombres décimaux et des caractères (lettres, signes de ponctuation,…).
Attention ! Ne confondez pas « système décimal » (utilisant les dix chiffres de 0 à 9) et « nombre décimal » (nombre qui contient une partie décimale et donc une virgule).
Quant à la numérisation des images et des sons, elle sera abordée dans le module qui leur est consacré.
En route pour les activités !