2. Le poids des images

Réflexions

Le poids

Le poids d'une image numérique équivaut à la taille du fichier qui lui correspond. Elle s'exprime donc le plus souvent en Ko ou en Mo.

Capteur CCD

Chaque cellule du capteur d'un appareil photo numérique génère un pixel. Ainsi, un appareil photo numérique dont le capteur comporte huit millions de cellules peut prendre une photo composée de huit millions de pixels (huit mégapixels). Cependant, il est possible, en faisant des réglages de l'appareil, de n'utiliser qu'une partie des cellules disponibles.

Scanneur

Un scanneur fonctionne de manière un peu différente, puisqu'il pratique par balayage du support à scanner. Les cellules sont alignées et la captation est réalisée progressivement pendant le balayage.

Dans l'un comme dans l'autre cas, plus le nombre de pixels est élevé, plus le poids des images produites est important. Logique ! À chaque pixel est associé une couleur, et chaque couleur est codée numériquement.

La profondeur

Plus l'image contient de couleurs différentes, plus le nombre de chiffres nécessaires pour coder chaque couleur est élevé. Le choix du nombre de chiffres binaires utilisé par un système informatique pour coder les couleurs va donc déterminer le nombre de couleurs pouvant être codées.

Le nombre de bits associé à chaque couleur est appelé profondeur de l'image.

Palette de 256 couleurs

Les couleurs ont longtemps été codées sur huit bits, c'est-à-dire sur un octet. Ce sont essentiellement les limites de capacité de stockage des supports qui en ont été la raison. Par ailleurs, des images lourdes prenaient du temps à être transférées et les vitesses de transfert n'étaient pas aussi élevées qu'elles le sont actuellement.

Vous le savez désormais, une image dont les couleurs sont codées sur un octet peut contenir jusqu'à 256 couleurs différentes.

On utilise souvent le mot « palette » pour désigner l'ensemble de ces couleurs en référence à la palette du peintre. Juste une petite différence, le peintre peut mélanger les couleurs. Un système informatique utilise les 256 couleurs de la palette, telles qu'elles.

Image A : codage des couleurs sur huit bits

Observons à nouveau la photo du balcon. Un système informatique l'a codée en utilisant huit bits pour identifier la couleur de chaque pixel.

On doit admettre que la qualité de l'image n'est pas exceptionnelle. Les transitions entre les couleurs sont assez brutales.

Image B : codage des couleurs sur vingt-quatre bits

Le même système a cette fois utilisé vingt-quatre bits pour l'image B.

Nous constatons que l'image est plus nette. Quelle en est la raison ?

Beaucoup plus de couleurs sont utilisées dans l'image B et donc, les nuances sont plus fines. Si on code chaque couleur sur un octet, on ne peut disposer que de 256 couleurs différentes pour reproduire l'image. Si on code chaque couleur sur trois octets, on dispose de plus de 16 millions de couleurs (256 x 256 x 256). Le dégradé des couleurs est donc beaucoup plus fin et l'image paraît plus nette.

Pourquoi avoir choisi de coder les couleurs sur 24 bits et non sur 16 ou 10 ou 20…? En avez-vous une idée ?

Voir la réponse

L’œil humain perçoit la lumière grâce à des cônes sensibles davantage au rouge, au vert ou au bleu.

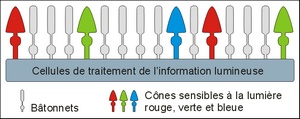Cônes et bâtonnets

C'est la raison pour laquelle les couleurs que nous percevons sont un mélange de ces trois couleurs fondamentales qu'il ne faut d'ailleurs pas confondre avec les couleurs fondamentales en peinture. Nous verrons plus loin pourquoi.

L'idée du codage des couleurs sur 24 bits (trois octets) a été d'utiliser un octet pour coder, non plus 256 couleurs différentes, mais 256 intensités différentes de chacune de trois couleurs de base.

Une couleur turquoise et ses trois composantes

Une couleur est donc définie comme un mélange en proportions diverses de rouge, de vert et de bleu.

Pour toutes ces raisons, les images codées en 24 bits ou trois octets sont dites images en vraies couleurs.

Interrogeons-nous maintenant sur l'évolution du poids des images avec la profondeur.

De quel facteur va augmenter le poids d'une image si on code ses couleurs en 24 bits au lieu de 8 bits ?

Voir la réponse

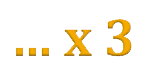
Réponse simple : d'un facteur 3.

Comme la couleur de chaque pixel est représentée par un nombre binaire trois fois plus grand, la longueur de la suite de nombres est multipliée par trois.

Ce qui doit nous étonner un peu, c'est qu'en augmentant d'un facteur trois le poids des images, on puisse augmenter le nombre de couleurs disponibles de 256 à plusieurs millions.

Observons maintenant les deux images qui suivent.

Image A

Image B

Les activités qui suivent vont vous permettre de mesurer le poids des images en fonction des choix de codage que vous pourriez faire.

Notez déjà que vos appareils photos numériques compressent vos photos avant de les stocker sur leur support. Mais cela, c'est une autre histoire dont nous reparlerons dans un des chapitres suivants.

La résolution

Les images ont besoin de supports pour pouvoir être admirées.

Pouvez-vous en citer quelques-uns ?

On peut les classer en deux grandes catégories. Voyez-vous lesquelles ?

Voir la réponse

Il y a les écrans LCD (ordinateurs, smartphones, iPads…) qui sont éclairés (apport direct de lumière) et les supports de type feuilles de papier, écran de projection, murs blancs… qui réfléchissent la lumière qu'ils reçoivent (qu'elle soit naturelle ou artificielle).

La qualité d'une image est liée à la densité des points (pixels) sur le support. Plus cette densité est élevée, plus l'image est nette. Et l'œil humain se satisfait d'une certaine densité, étant donné son pouvoir séparateur.

Cela dit, une image étant composée d'un nombre déterminé de pixels, plus la densité de ces pixels est élevée sur le support, et plus l'image sera petite. Vous verrez, dans les activités, en quoi cette densité, aussi appelée résolution, est variable d'un support à l'autre et quelles en sont les conséquences.